SENTENTIAL LOGIC

0.0

A very special island is inhabited only by knights and knaves. Knights always tell the truth, and knaves always lie.

You meet Zoey and Peggy. Zoey tells you that they both are knaves.
Can you determine if Zoey is a knight or a knave?

You meet Zoey and Peggy. Zoey tells you that at least one of them is a knave.
Can you determine if Zoey is a knight or a knave?

0.1

A very special island is inhabited only by knights and knaves. Knights always tell the truth, and knaves always lie.

You meet two inhabitants: Zoey and Mel. Zoey tells you that Mel is a knave. Mel says, “Neither Zoey nor I are knaves.”

Can you determine who is a knight and who is a knave?

 

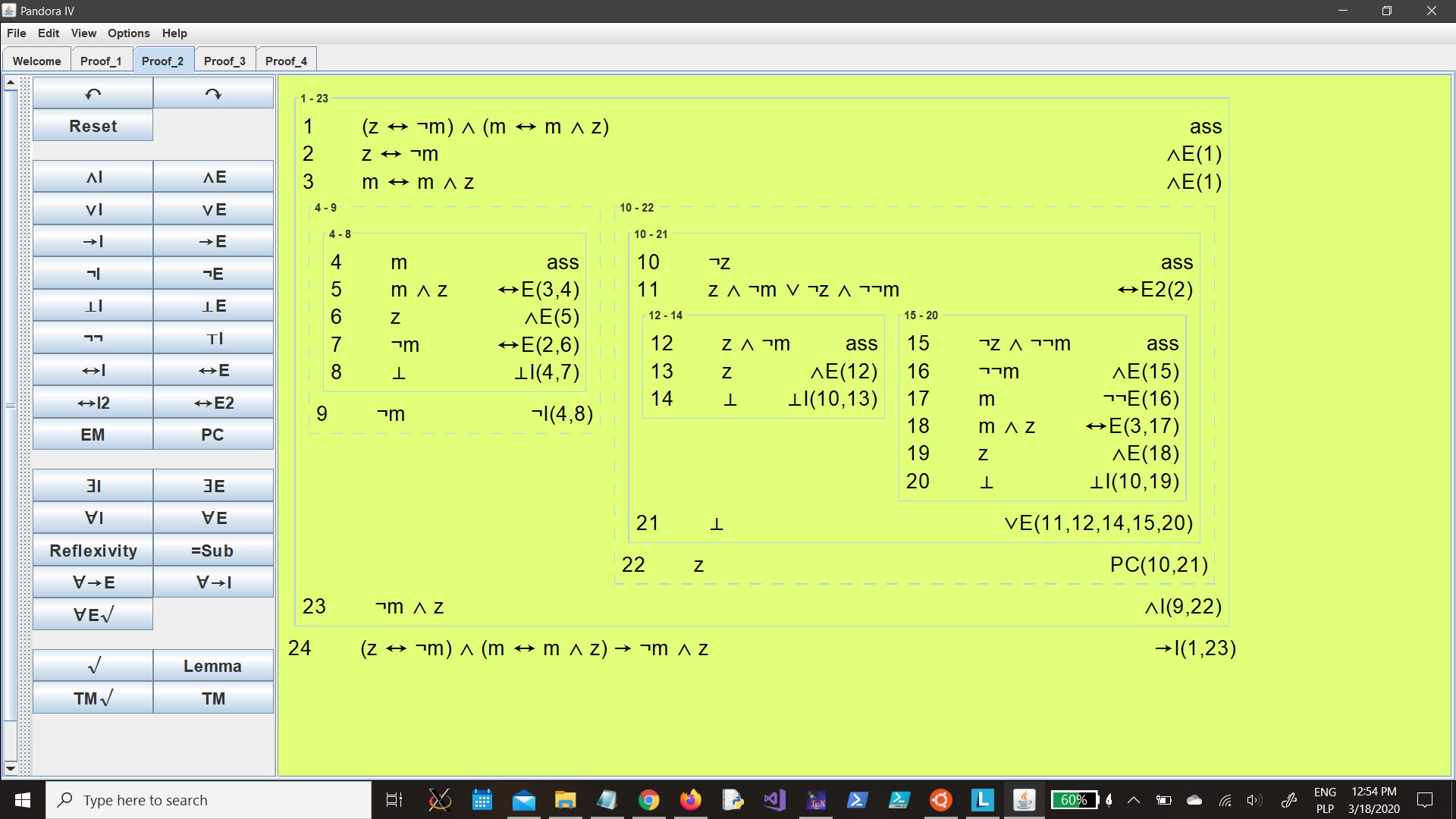
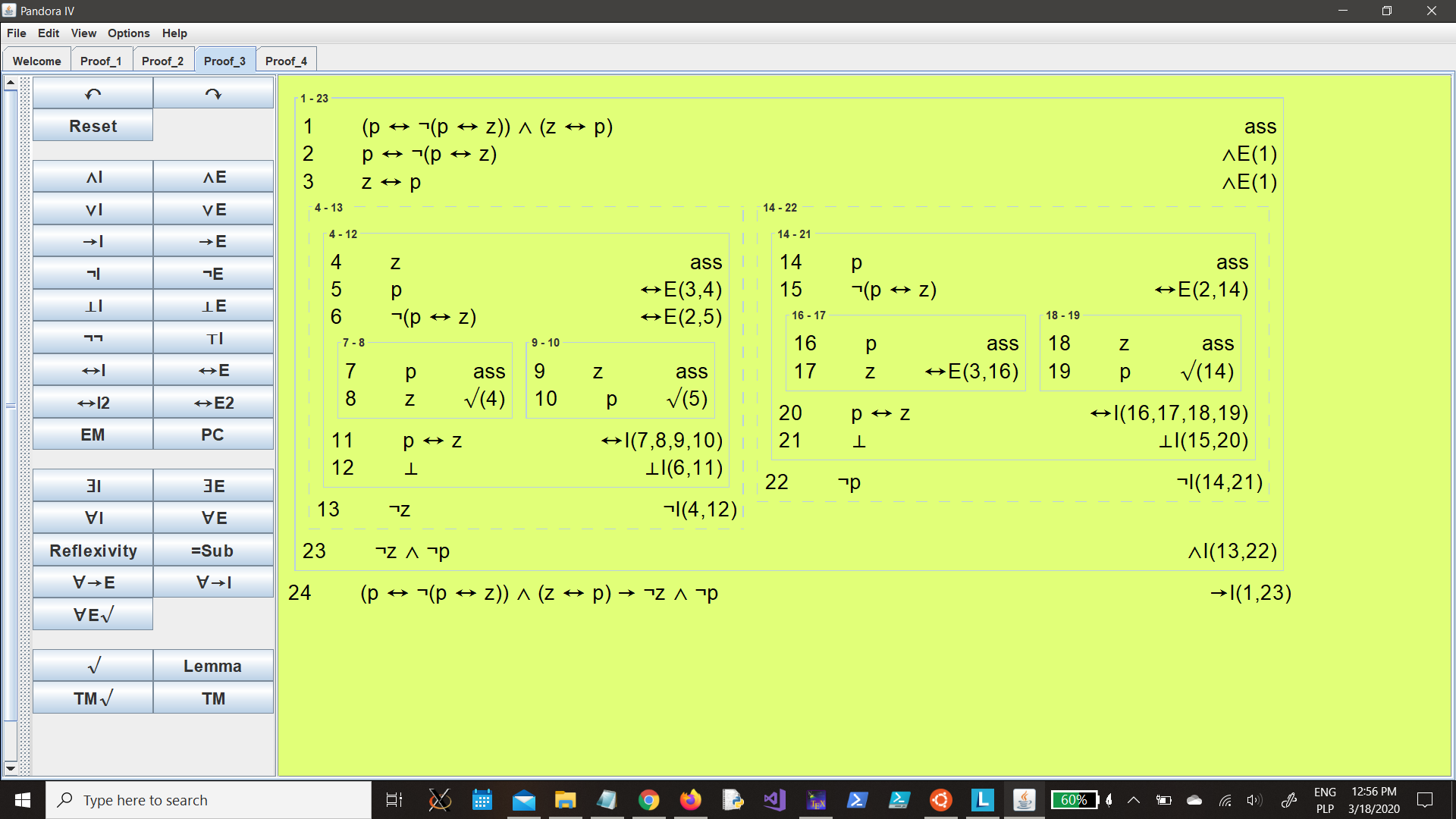
0.2

A very special island is inhabited only by knights and knaves. Knights always tell the truth, and knaves always lie.

You meet two inhabitants: Peggy and Zippy. Peggy tells you that “of Zippy and I, exactly one is a knight’. Zippy tells you that only a knave would say that Peggy is a knave.

Can you determine who is a knight and who is a knave?

 

I

A very special island is inhabited only by knights and knaves. Knights always tell the truth, and knaves always lie. You meet four inhabitants: Dave, Rex, Bart and Zoey. Dave tells you that Bart could say that Rex is a knave. Rex claims, `I would tell you that Bart is a knave.’ Bart claims, `Only a knave would say that Zoey is a knave.’ Zoey claims, `I and Dave are different.’

II

A very special island is inhabited only by knights and knaves. Knights always tell the truth, and knaves always lie. You meet four inhabitants: Bart, Dave, Rex and Zoey. Bart tells you that Rex and Dave are both knights or both knaves. Dave tells you that Zoey is a knave. Rex claims, `Bart is a knave.’ Zoey claims, `Rex is a knight and Dave is a knave.’

In case of encountering problems click here!

III

A very special island is inhabited only by knights and knaves. Knights always tell the truth, and knaves always lie.

The local police conducts an investigation about a robbers’ attack at the National Bank.

They interrogated six inhabitants: Betty, Rex, Peggy, Carl, Zeke and Marge. Betty claims that Marge is a knave. Rex tells you that Zeke could say that Peggy is a knight. Peggy tells you, “Only a knave would say that Marge is a knave.” Carl tells you that either Marge is a knight or Peggy is a knight. Zeke tells you, “Neither Marge nor Rex are knights.” Marge claims that it’s not the case that Rex is a knave.

Finally, Carl tells you that if Peggy is a thief (that is, she robbed the bank) then Zeke helped her (she is a thief as well). But Zeke claims that it is Carl who is a thief.

Your task is to solve the puzzle: who robbed the bank?

In case of encountering problems click here!

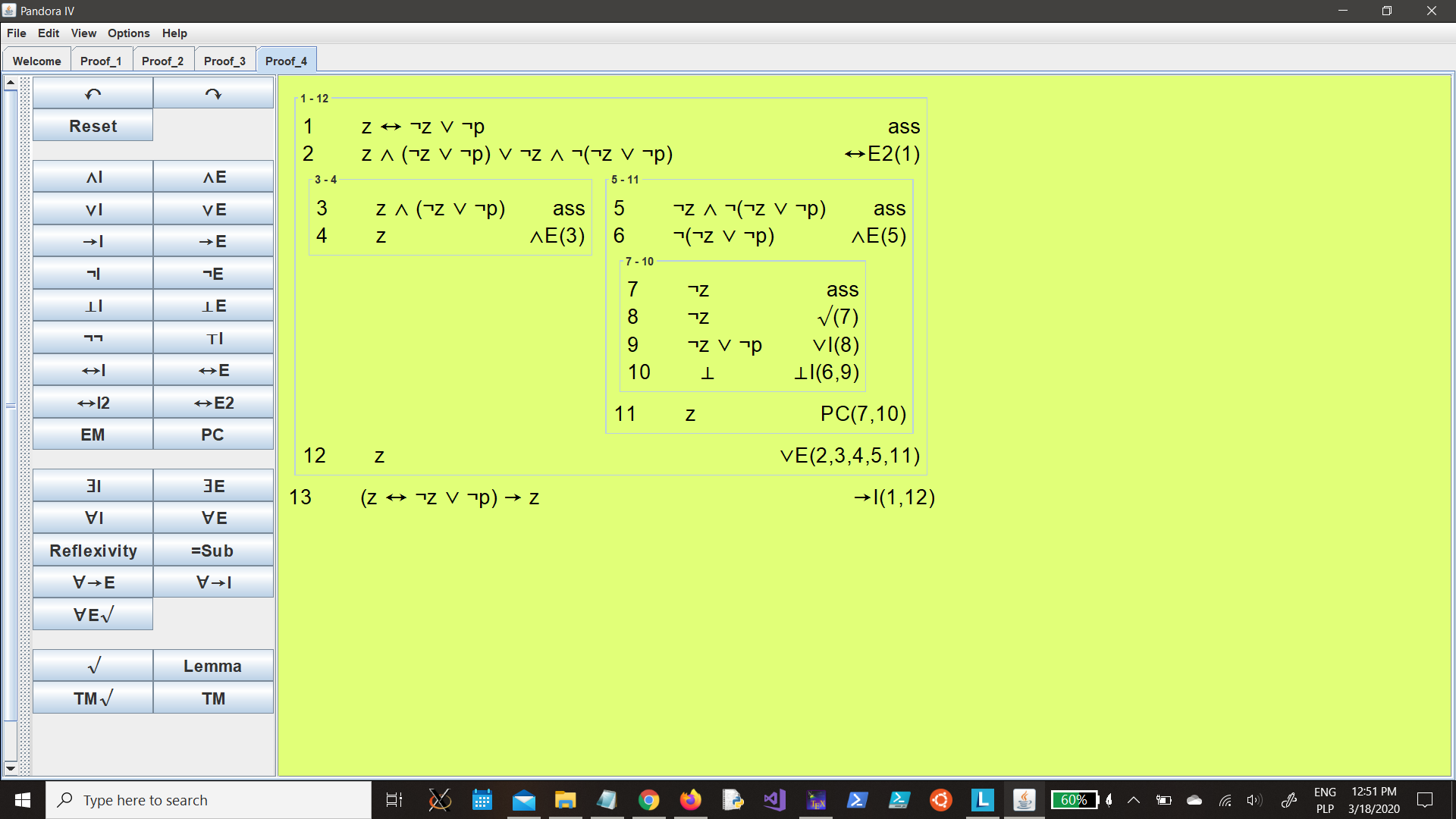
IV

A very special island is inhabited only by knights and knaves. Knights always tell the truth, and knaves always lie.

The local police conducts an investigation about a robbers’ attack at the National Bank.

You meet seven inhabitants: Ted, Alice, Zed, Marge, Zippy, Sally and Betty. Ted tells you that Alice is a knave. Alice says that Sally is a knight or Zed is a knight. Zed claims that Alice could claim that Betty is a knight. Marge claims, “It’s false that Betty is a knave.” Zippy says that only a knave would say that Ted is a knave. Sally claims, “I am a knight or Betty is a knave.” Betty says that Zippy is a knave or Ted is a knave.

Finally, Sally says that if Zippy is a thief then Zed is a knight. Alice says that if Sally is a knight then Sally is a thief. And Zed claims that if Sally is wrong, then Marge is a thief.

As always, your task is to solve the puzzle: who robbed the bank?

In case of encountering problems click here!

 

I-ORDER LOGIC

I

Wiesz, że każda kiężniczka jest żabą, ale nie każda żaba jest księżniczką. Tylko księżniczki są piękne. Każdy kto jest piękny nie jest brzydki, a kto nie jest brzydki jest piękny.

• Czy istnieją księżniczki?
• Czy istnieją brzydkie księżniczki?
• Czy istnieją piękne księżniczki?
• Czy istnieją żaby?
• Czy istnieją brzydkie żaby?
• Czy istnieją piękne żaby?

II

Wiesz, że nikt nie jest żabą lub każdy jest księciem.

• Czy jeżeli Mirmił jest żabą to Kermit księciem?
• Czy jeżeli Mirmił jest księciem to Kermit jest żabą?
• Czy jeżeli Mirmił nie jest księciem to Kermit nie jest żabą?
• Czy jeżeli Mirmił jest żabą to jeżeli jest także księciem to Kermit jest żabą?
• Czy jeżeli Mirmił jest żabą to jeżeli nie jest także księciem to Kermit jest żabą?

III

Wiesz, że każdy jest kobietą. Każda kobieta jest wieśniaczką lub księżniczką. Nie tylko księżniczki są piękne i nie tylko wieśniaczki są brzydkie. Każdy kto jest piękny nie jest brzydki, a kto nie jest brzydki jest piękny.

• Czy instnieje piękna księżniczka?
• Czy istenieje brzydka księżniczka?
• Czy instnieje piękna wieśniaczka?
• Czy instnieje brzydka wieśniaczka?

IV

Fakt: Tylko ludzie którzy nie są ani bogaci ani sławni są logikami. Każdy kto ma milion PLN jest bogaty. Czy logicy mają milion PLN?

V

Fakt: Nie istnieje nikt taki ze jeżeli jest brzydki to jest żabą.

• Czy każda królewna jest żaba?
• Czy każda królewna jest brzydka?
• Czy żadna królewna nie jest żaba?
• Czy jeżeli Gargamel jest brzydki to jest żaba czy też nie jest?

VI

Fakt: Każdy królewicz kocha jakąś piekną królewną. Tylko królewny nie są piąkne. Królewna Śnieżka nie jest piękna a Mirmił jest królewiczem.

• Czy istnieją co najmniej dwaj królewicze?
• Czy istnieją co najmniej dwie królewny?
• Czy Mirmił kocha Śnieżkę?
• Czy Mirmił nie kocha Śnieżki?
• Czy Mirmił kocha kogoś innego niż Śnieżka?

VII

Wiesz że święci ludzie są szczęśliwi oraz że Karol jest czczony ale nie jest szczęśliwy. Wiesz również że każdy jest święty lub jest potępiony. (Sygnatura: symbole relacyjne: czczony(x), potępiony(x), święty(x), szczęśliwy(x); stałe: Karol).

• Czy ktoś jest czczony choć jest potępiony?
• Czy ktoś jest potępiony choć czczony?
• Czy każdy potępiony nie jest szczęśliwy?
• Czy każdy kto nie jest potępiony jest szczęśliwy?

VIII

Szalony turniej rycerski: dla każdego losowany jest giermek i rywal (nie ma żadnych ograniczen nałożonych na te funkcje). Zatem wiesz że każdy ma jakiegoś (jednego) rywala i każdy ma jakiegoś (jednego) giermka.

SYGNATURA: symbole funkcyjne: rywal(x), giermek(x).

• Jeżeli istnieje ktoś kto jest rywalem wszystkich, to dowolni dwaj rycerze mają tego samego rywala.
• Jeżeli dowolni dwaj rycerze mają tego samego rywala, to istnieje ktoś kto jest rywalem wszystkich.
• Jeżeli dowolni dwaj rycerze którzy są różni mają różnych giermków, to każdy jest giermkiem swojego giermka.
• Jeżeli każdy jest giermkiem swojego giermka, to dowolni dwaj rycerze którzy są różni mają różnych giermków.

IX

Sygnatura: symbole funkcyjne: miks (2-arg), rozcieńczenie (1-arg); symbole relacyjne 1-arg: dobry. Udowodnij, że:

• Jeżeli istnieje drink który jest miksem dowolnych dwóch drinków, to każde dwa miksy dowolnych drinków są identyczne.
• Jeżeli istnieją dwa drinki takie, że rozcieńczenie jednego z nich jest dobre a rozciecieńczenie drugiego takie nie jest, to istnieją dwa drinki których rozcieńczenia są rózne.

X

Udowodnij, że:

• Każda zwrotna relacja Euklidesowa jest symetryczna.
• Każda zwrotna relacja Euklidesowa jest przechodnia.
• Każda relacja równoważności jest relacją Euklidesową.

 

PEANO ARITHMETIC

My notes:

Ax[Ay[s(x)=s(y)->x=y]]^
Ax[~s(x)=zero]^
Ax[plus(x,zero)=x]^
Ax[Ay[plus(x,s(y))=s(plus(x,y))]]^
Ax[times(x,zero)=zero]^
Ax[Ay[times(x,s(y))=plus(times(x,y),x)]]

Ax[Ay[plus(plus(x,y),zero)=plus(x,plus(y,zero))]]^
Ax[Ay[Az[plus(plus(x,y),z)=plus(x,plus(y,z))->plus(plus(x,y),s(z))=plus(x,plus(y,s(z)))]]]->Ax[Ay[Az[plus(plus(x,y),z)=plus(x,plus(y,z))]]]

Ax[plus(s(x),zero)=plus(x,s(zero))]^
Ax[Ay[plus(s(x),y)=plus(x,s(y))->plus(s(x),s(y))=plus(x,s(s(y)))]]->
Ax[Ay[plus(s(x),y)=plus(x,s(y))]]

Ax[plus(x,zero)=plus(zero,x)]^
Ax[Ay[plus(x,y)=plus(y,x)->plus(x,s(y))=plus(s(y),x)]]->
Ax[Ay[plus(x,y)=plus(y,x)]]

plus(zero,zero)=plus(zero,zero)^Ax[plus(x,zero)=plus(zero,x)->plus(x,s(zero))=plus(s(zero),x)]->Ax[plus(x,zero)=plus(zero,x)]

 

Proofs of associative and commutative properties of addition; the latter one needs a corollary:

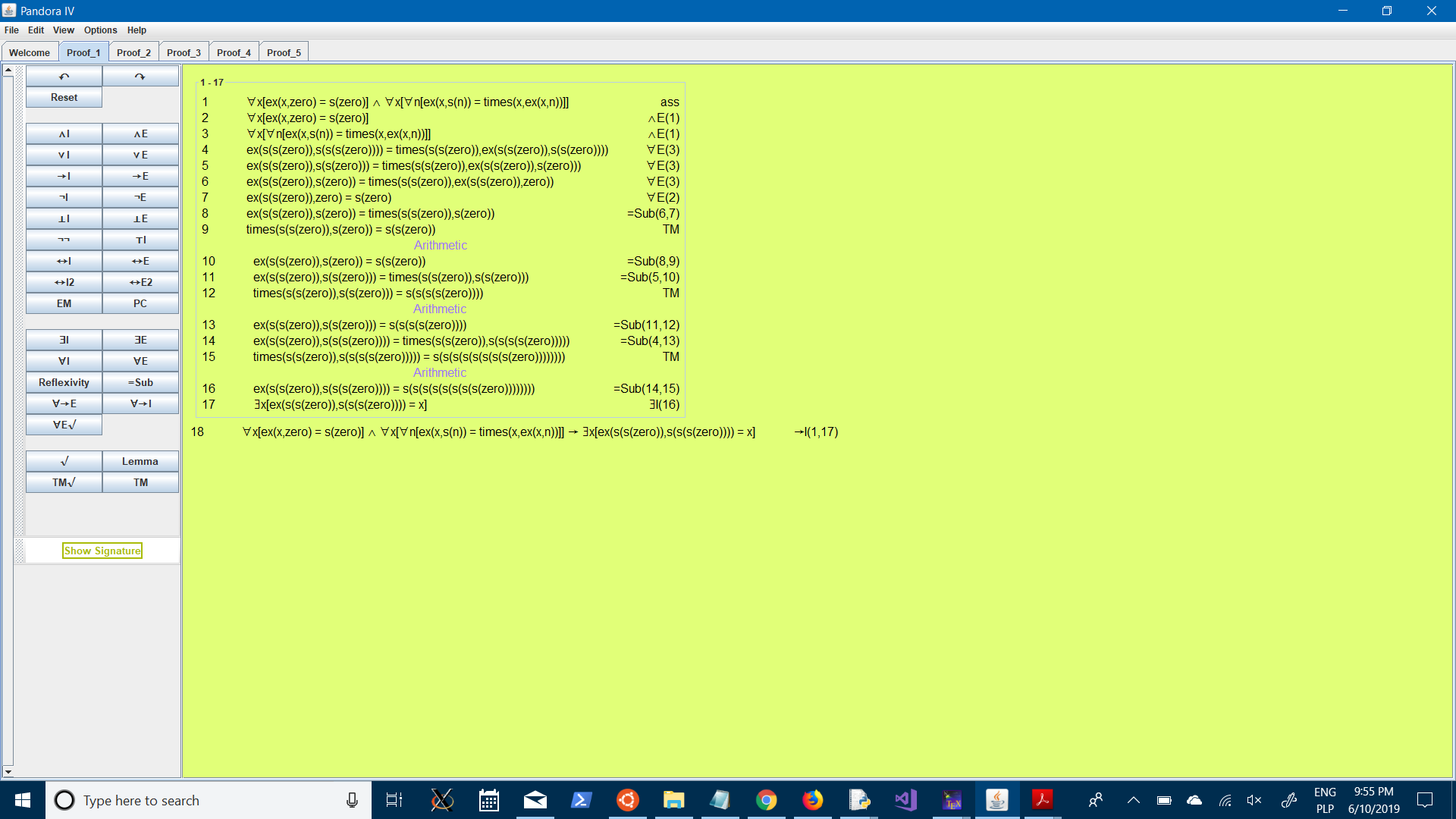
The associative property:

 

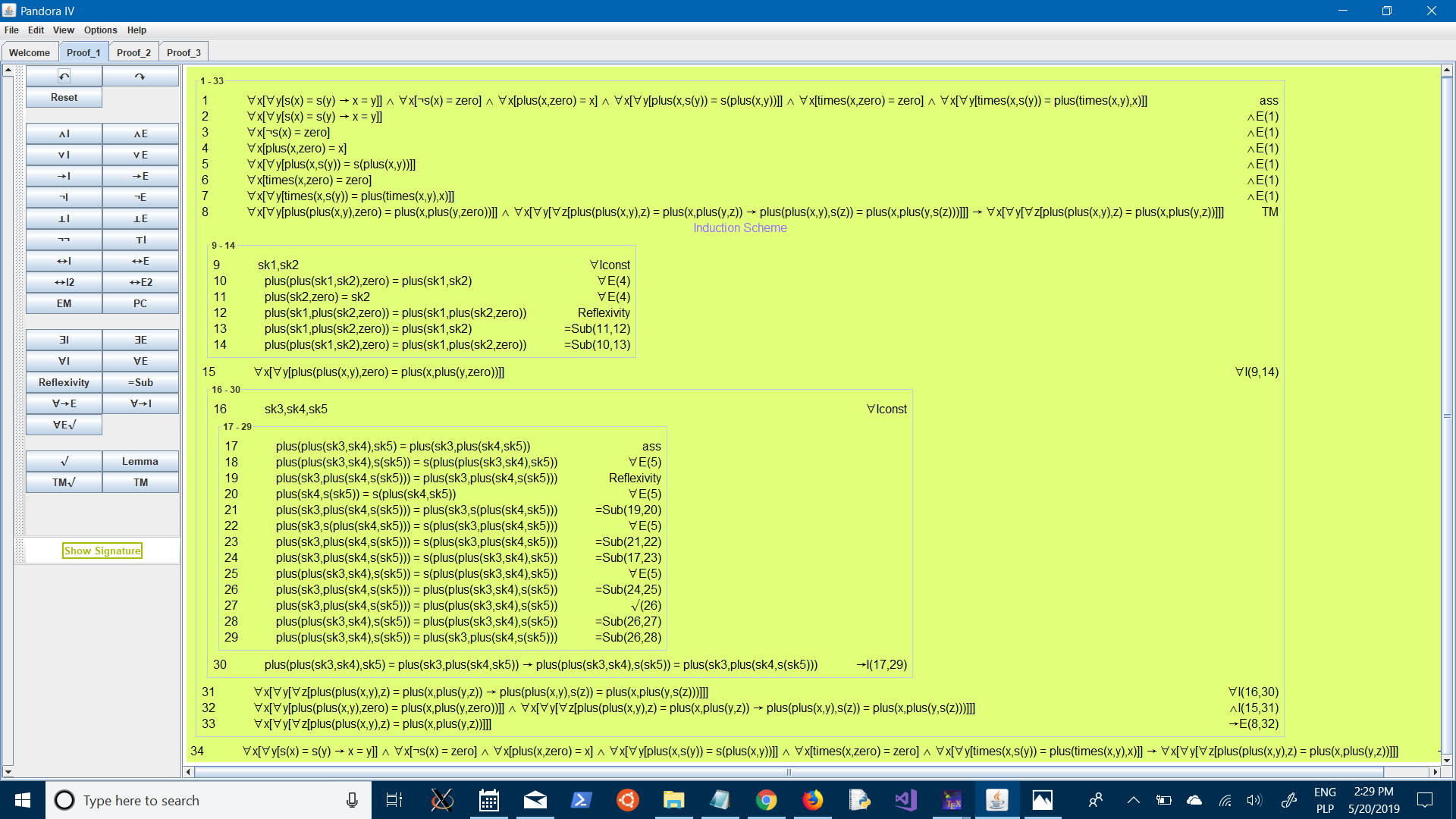
Lemma:

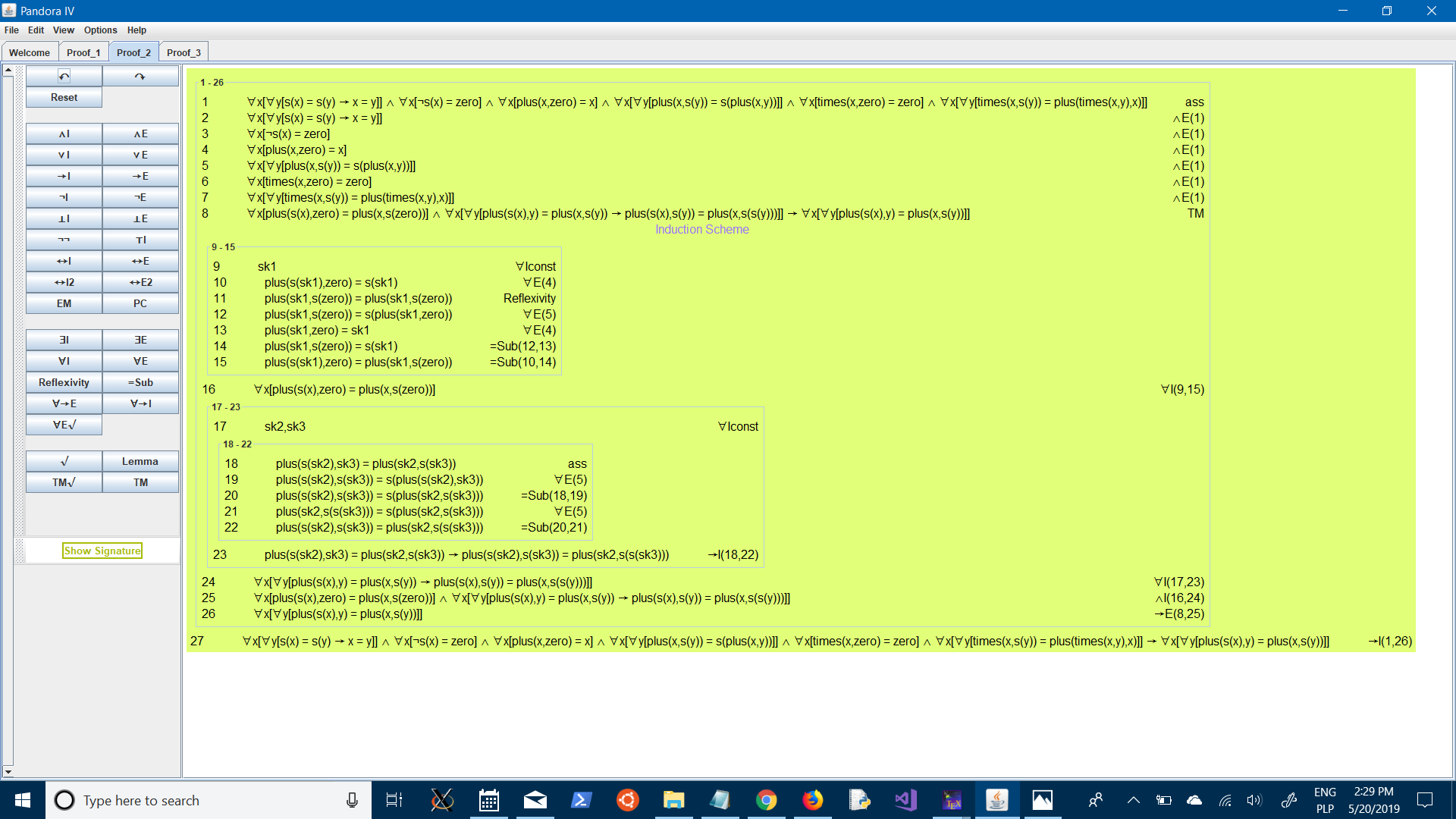
The commutative property:

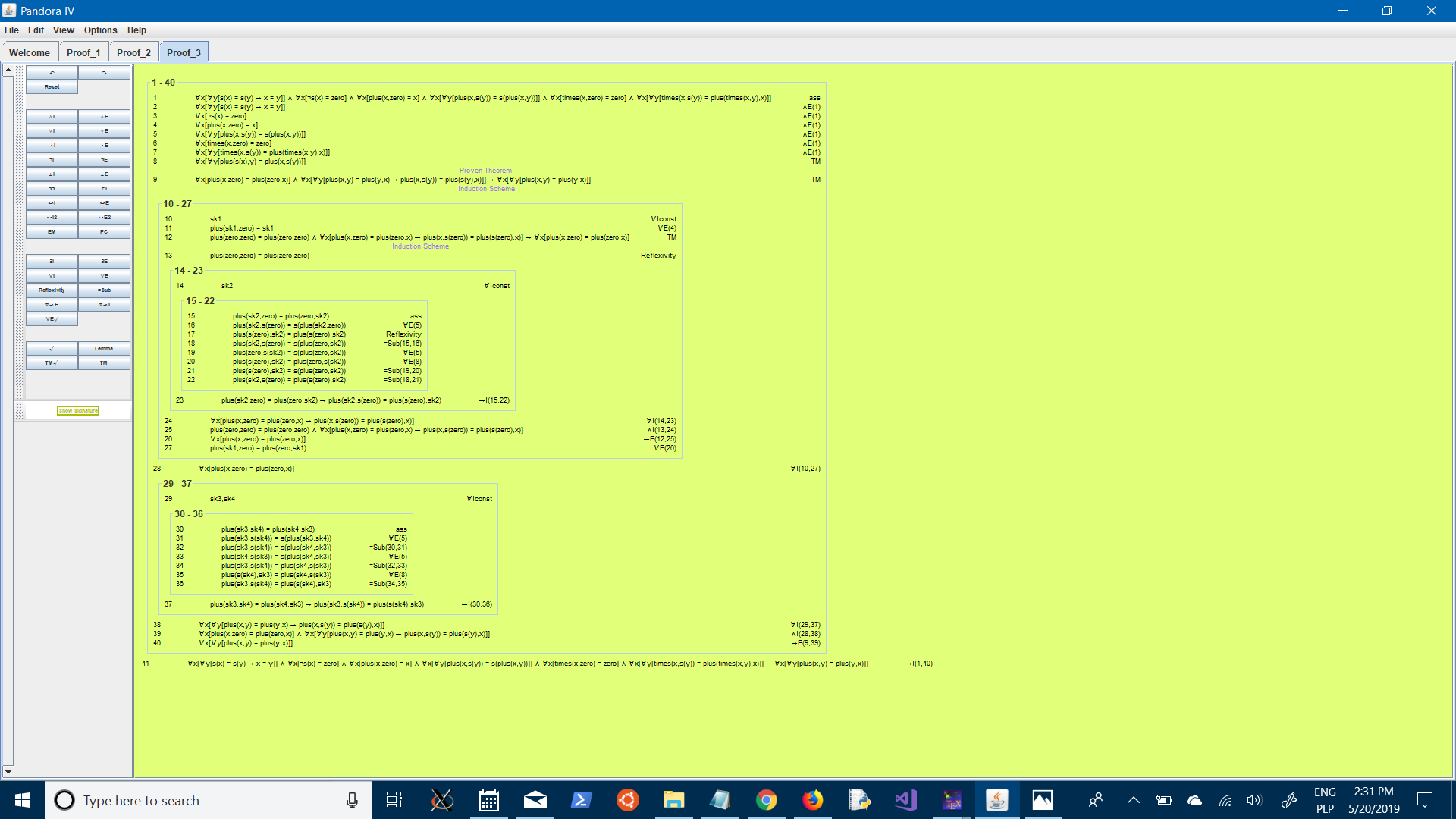
PROGRAMMING

 

def power(a,n):
 if n == 0:
   return 1
 else:
   return a * power(a,n - 1)

def power(a,n):
 result=1
 for i in range(n):
   result = result * a
 return result

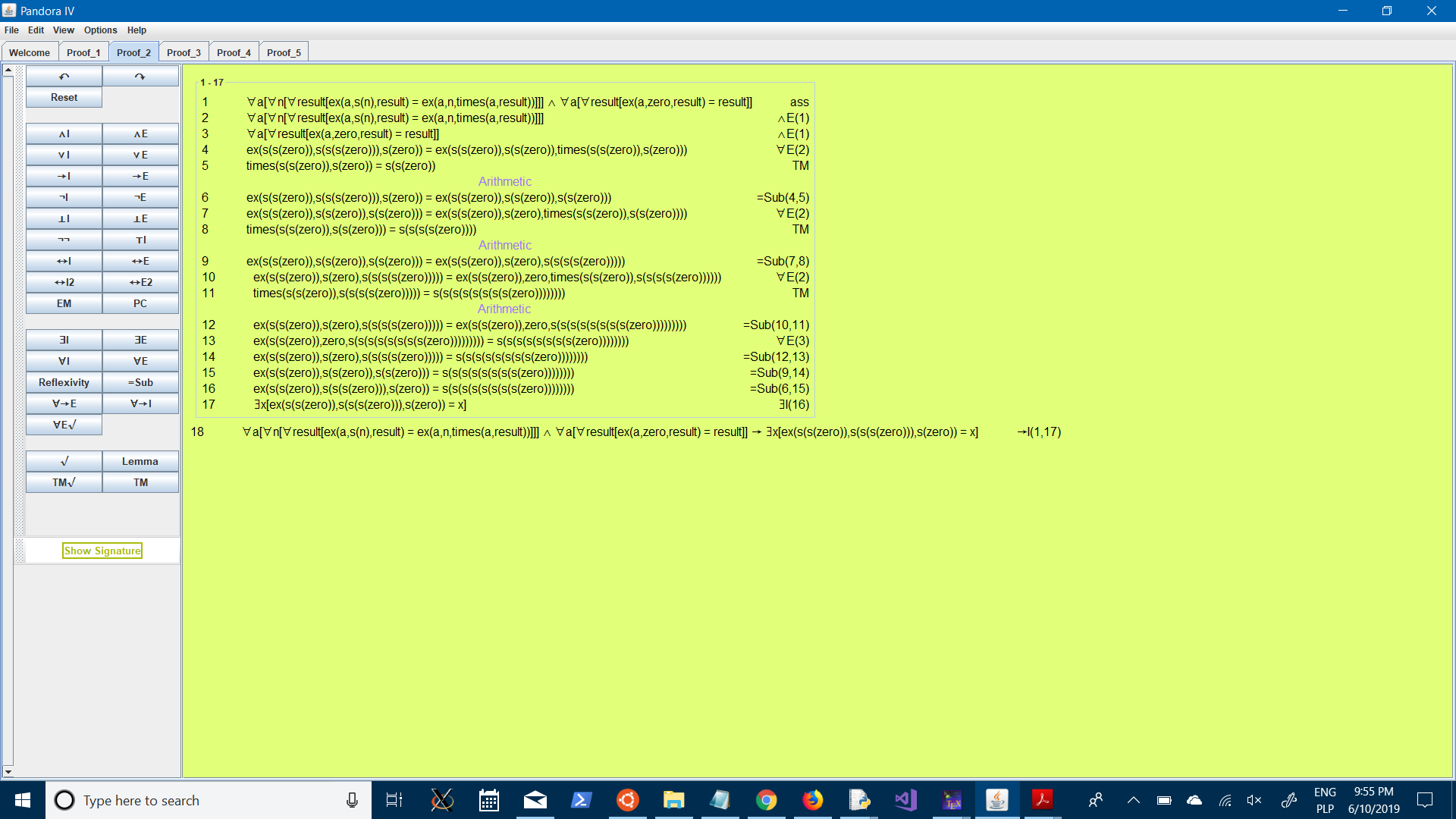
def power(a,n,result=1):
 if n==0:
   return result
 else:
   return power(a,n-1,a*result)

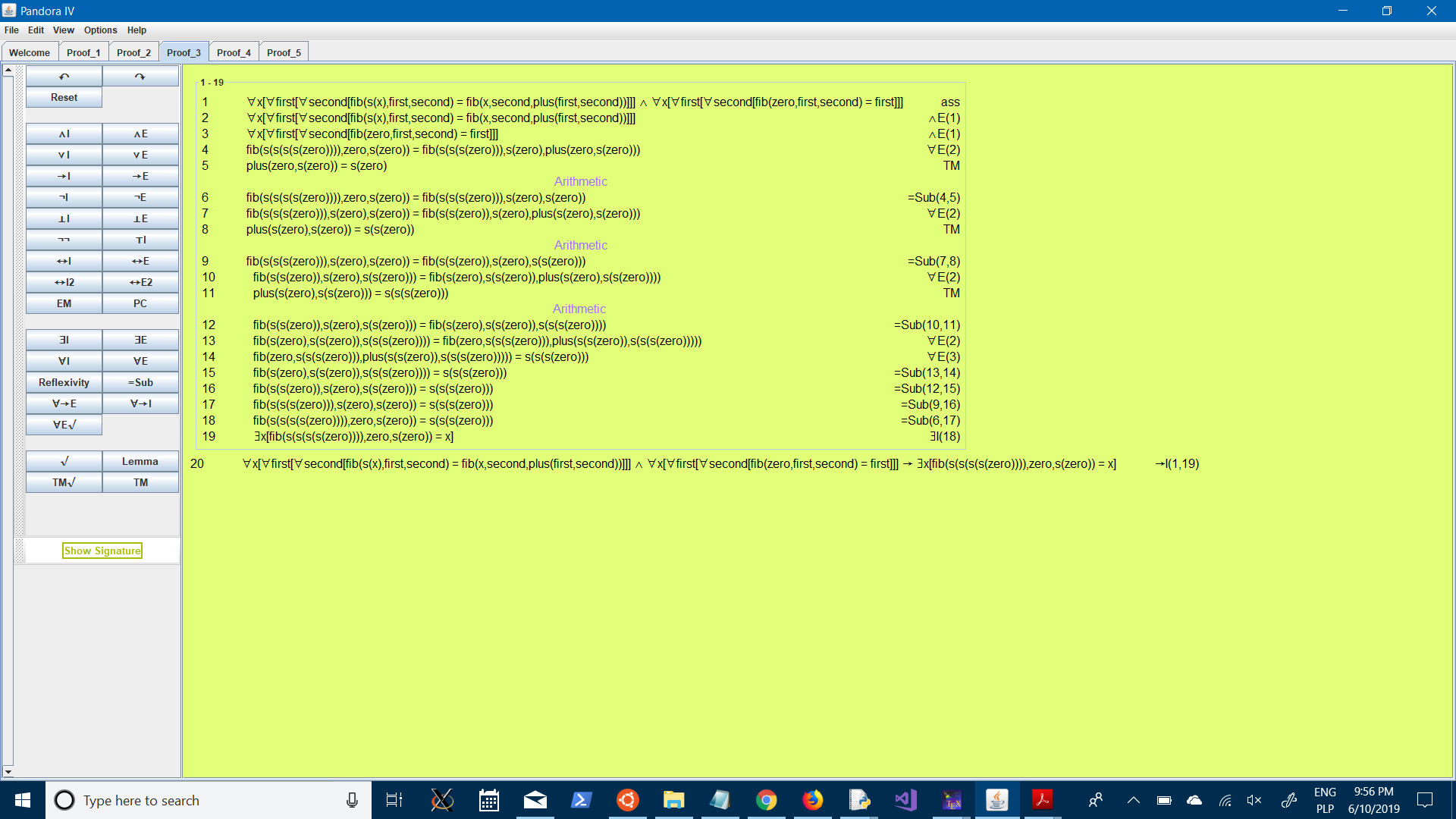
def Fibo(x):
 if x == 0 or x == 1:
   return x
 else:
   return Fibo(x-1) + Fibo(x-2)

def Fibo(x):
 first=0
 second=1
 for i in range(x):
   temp = first
   first = second
   second = temp + first
 return first

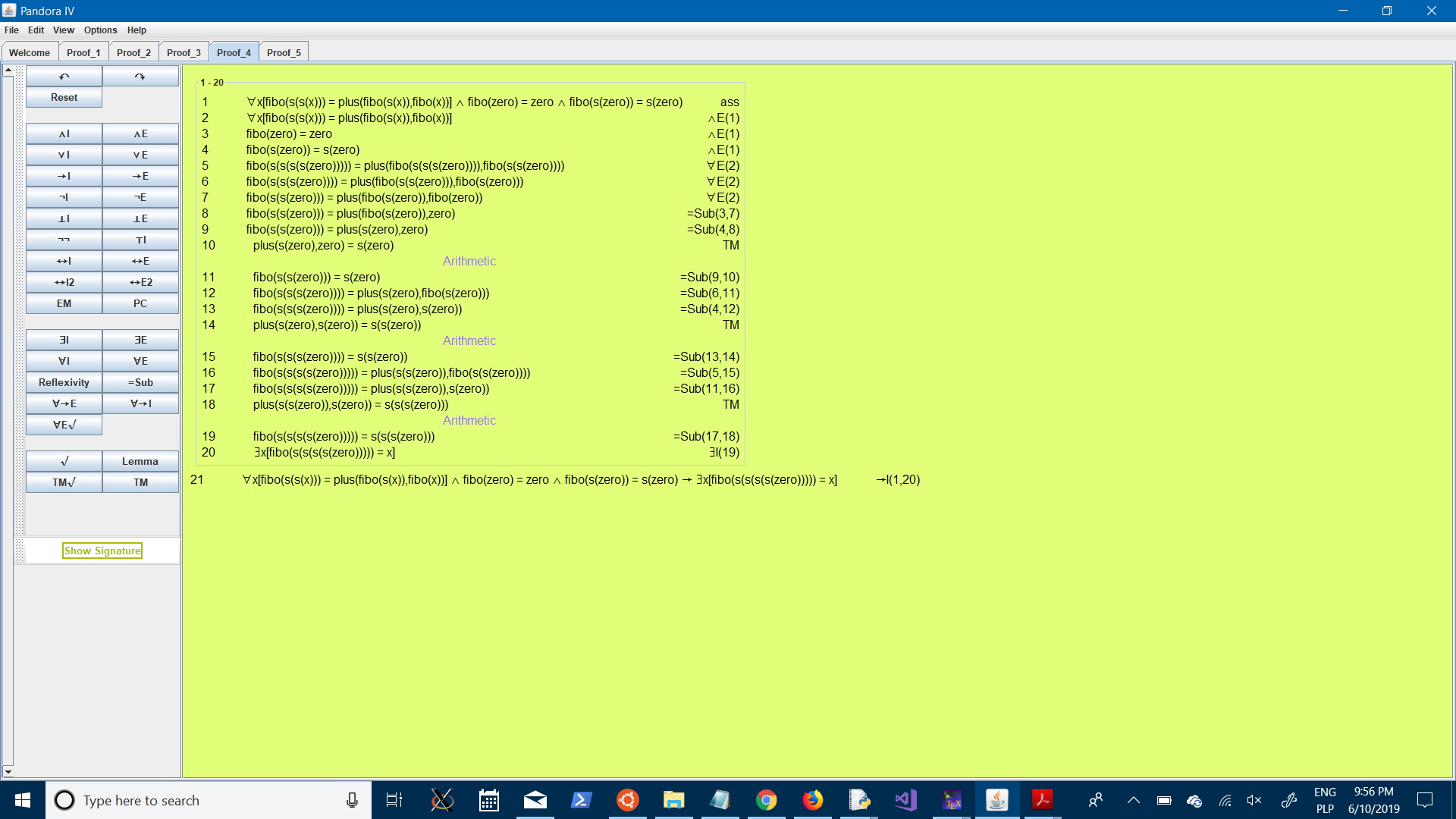
def Fibo(x,first=0,second=1):
 if x == 0:
   return first
 else:
   return Fibo3(x-1,second,first+second)
 
def Hanoi(n,start=1,park=2,stop=3):
 if n==1:
   print("Move the top disk of Tower {} to the Tower {}.".format(start,stop))
 else:
   Hanoi(n-1,start,stop,park)
   Hanoi(1,start,park,stop)
   Hanoi(n-1,park,start,stop)